#2 dsacpp
目录
vector
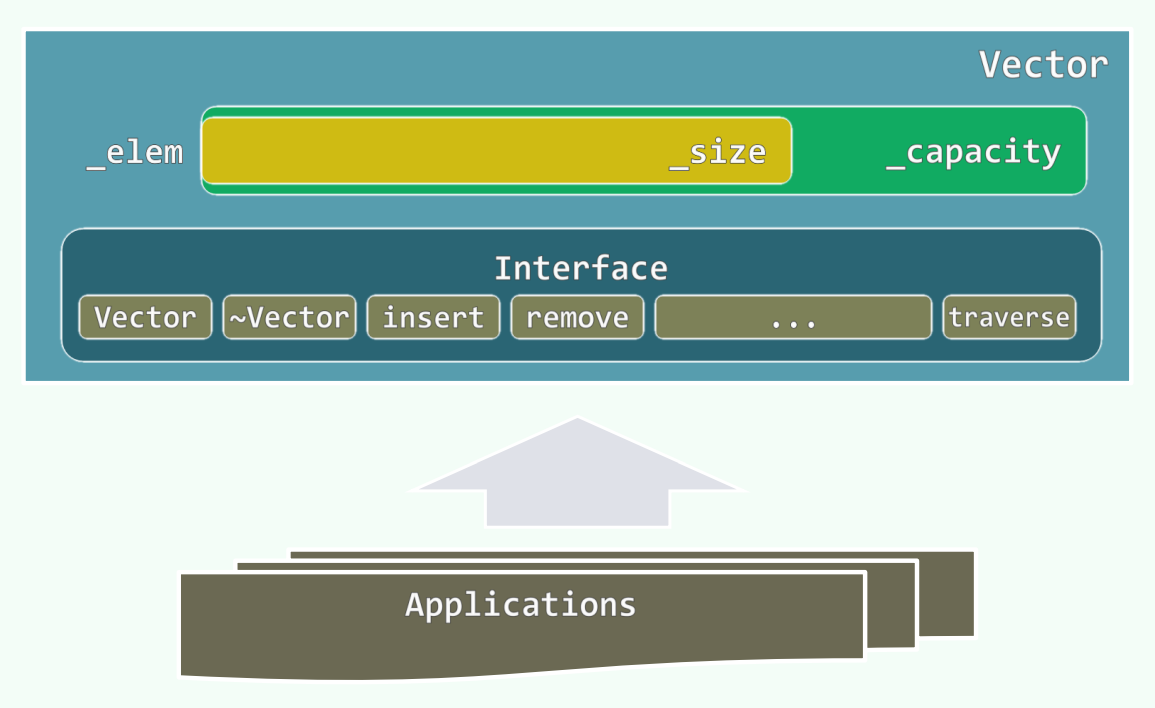
vector模板类
// vector.h
#pragma once
#include <functional>
// 用于函数指针
using Rank = unsigned int; //秩
#define DEFAULT_CAPACITY 3 //默认的初始容量(实际应用中可设置为更大)
template <typename T> class Vector { //向量模板类
protected:
Rank _size; Rank _capacity; T* _elem; //规模、容量、数据区
void copyFrom(T const* A, Rank lo, Rank hi); //复制数组区间A[lo, hi)
void expand(); //空间不足时扩容
void shrink(); //装填因子过小时压缩
bool bubble(Rank lo, Rank hi); //扫描交换
void bubbleSort(Rank lo, Rank hi); //起泡排序算法
Rank maxItem(Rank lo, Rank hi); //选取最大元素
void selectionSort(Rank lo, Rank hi); //选择排序算法
void merge(Rank lo, Rank mi, Rank hi); //归并算法
void mergeSort(Rank lo, Rank hi); //归并排序算法
void heapSort(Rank lo, Rank hi); //堆排序(稍后结合完全堆讲解)
Rank partition(Rank lo, Rank hi); //轴点构造算法
void quickSort(Rank lo, Rank hi); //快速排序算法
void shellSort(Rank lo, Rank hi); //希尔排序算法
public:
// 构造方法
Vector(Rank c = DEFAULT_CAPACITY) //容量为c的空向量
{
_elem = new T[_capacity = c]; _size = 0;
}
Vector(Rank c, Rank s, T v) //容量为c、规模为s、所有元素初始为v;s<=c
{
_elem = new T[_capacity = c]; for (_size = 0; _size < s; _elem[_size++] = v);
}
Vector(T const* A, Rank n) { copyFrom(A, 0, n); } //数组整体复制
Vector(T const* A, Rank lo, Rank hi) { copyFrom(A, lo, hi); } //区间
Vector(Vector<T> const& V) { copyFrom(V._elem, 0, V._size); } //向量整体复制
Vector(Vector<T> const& V, Rank lo, Rank hi) { copyFrom(V._elem, lo, hi); } //区间
// 析构方法
~Vector() { delete[] _elem; } //释放内部空间
// 只读访问接口
Rank size() const { return _size; } //规模
bool empty() const { return !_size; } //判空
Rank find(T const& e) const { return find(e, 0, _size); } //无序向量整体查找
Rank find(T const& e, Rank lo, Rank hi) const; //无序向量区间查找
Rank select(Rank k) { return quickSelect(_elem, _size, k); } //从无序向量中找到第k大的元素
Rank search(T const& e) const //有序向量整体查找
{
return (0 >= _size) ? -1 : search(e, 0, _size);
}
Rank search(T const& e, Rank lo, Rank hi) const; //有序向量区间查找
// 可写访问接口
T& operator[] (Rank r); //重载下标操作符,可以类似于数组形式引用各元素
const T& operator[] (Rank r) const; //仅限于做右值的重载版本
Vector<T>& operator= (Vector<T> const&); //重载赋值操作符,以便直接克隆向量
T remove(Rank r); //删除秩为r的元素
Rank remove(Rank lo, Rank hi); //删除秩在区间[lo, hi)之内的元素
Rank insert(Rank r, T const& e); //插入元素
Rank insert(T const& e) { return insert(_size, e); } //默认作为末元素插入
void sort(Rank lo, Rank hi); //对[lo, hi)排序
void sort() { sort(0, _size); } //整体排序
void unsort(Rank lo, Rank hi); //对[lo, hi)置乱
void unsort() { unsort(0, _size); } //整体置乱
Rank disordered(); // 逆序对个数
Rank deduplicate(); //无序去重
Rank uniquify(); //有序去重
// 遍历
void traverse(std::function<void(T&)> visit); //遍历(使用函数指针,只读或局部性修改)
template <typename VST> void traverse(VST&); //遍历(使用函数对象,可全局性修改)
}; //Vector
真正的Vevtor是封装起来的 用户只能使用接口
可以通过模板参数T 指定向量元素的类型 比如Vector<int> 而Vector<Vector<char>>就是存放char的二维数组 第1维和第2维的大小都不固定 Vector<int> a[maxn]二维数组 第1维(行)的大小是固定的maxn 第2维(列)的大小不固定
构造
using Rank = unsigned int;
头文件Vector模板类中 Rank _size; Rank _capacity; T* _elem; 是维护了一个元素为T类型的protected数组_elem[] 虽然它存储的是指针
向量中秩为r的元素 对应于内部数组中的_elem[r] 其物理地址为_elem+r 指针算数已经隐含了其实是_elem+r*sizeof(T)字节 但不允许这样写 只能写_elem+r 编译器会自动处理
Vector ( Rank c = DEFAULT_CAPACITY ) //容量为c的空向量
{
_elem = new T[_capacity = c];
_size = 0;
}
Vector ( Rank c, Rank s, T v ) //容量为c、规模为s、所有元素初始为v;s<=c
{
_elem = new T[_capacity = c];
for ( _size = 0; _size < s; _elem[_size++] = v );
}
基于复制的构造
Vector ( T const* A, Rank n ) //数组整体复制
{
copyFrom ( A, 0, n );
}
const T* a或者T const* a
表示a是一个指向const T类型数据的指针 指针a本身不是常量 因此可以重新指向其他地址 但*a是常量 无法对*a进行修改
实际上这个指针就是数组了
使用常量 使得这个方法既可以接收左值 也可以接收右值
Vector ( T const* A, Rank lo, Rank hi ) //数组区间复制
{
copyFrom ( A, lo, hi );
}
Vector ( Vector<T> const& V ) //向量整体复制
{
copyFrom ( V._elem, 0, V._size );
}
Vector ( Vector<T> const& V, Rank lo, Rank hi ) //向量区间复制
{
copyFrom ( V._elem, lo, hi );
}
copyFrom重载了很多形式 所以可以从数组复制 也可以从向量复制
copyFrom 区间复制
// vector_copyFrom.h
#pragma once
#include "vector.h"
template <typename T>
void Vector<T>::copyFrom(T const* A, Rank lo, Rank hi)
{
_elem = new T[_capacity = 2 * (hi - lo)]; // 开辟了两倍的空间 接下来很长一段时间内 不必因为扩容而打断计算过程
_size = 0; // 先将规模置为0
while (lo < hi)
_elem[size++] = A[lo++];
}
描述区间往往是用左闭右开 [lo,hi)
所以现在就是将A[lo,hi)中的元素逐一复制到_elem[0,hi-lo)
重载operator=
向量之间赋值 如果T不是基本数据类型 就需要重载operator=
// vector_operator_assignment.h
#pragma once
#include "vector.h"
template <typename T>
Vector<T>& Vector<T>::operator= (Vector<T> const& V)
{
if (_elem) delete[] _elem; // 释放_elem原有内容
copyFrom(V._elem, 0, V.size());
return *this;
}
析构
~Vector()
{
delete [] _elem;
}
expand 扩容

前面介绍的向量 并不具备可扩充的性能 因为它用的是静态空间管理 内部只不过是开辟了数组 占用了一段连续的物理空间
_size 元素的总数 占用的逻辑空间数
_capacity 占用的物理空间数
静态空间管理策略 _capacity是固定的
上溢 overflow _elem[]不足以存放所有元素
下溢 underflow _elem[]中的元素太少
容量已满的时候 就申请一块新内存 开辟一块新的空间 把旧的内存复制到新内存 并将旧内存所在的空间释放
// vector_expand.h
#pragma once
#include "vector.h"
template <typename T>
void Vector<T>::expand()
{
if (_size < _capacity)
return; // 容量未满的时候无需扩容 否则扩容
_capacity = max(_capacity, DEFAULT_CAPACITY); // 不低于最小容量
T* oldElem = _elem;
_elem = new T[_capacity <<= 1]; // 移位 新开辟一块内粗 容量加倍
for (int i = 0; i < _size; i++)
_elem[i] = oldElem[i]; // 逐一复制原来的元素 要求T为基本类型 或者已经重载操作符=
delete[] oldElem; // 释放原空间
}
重载operator[]
循秩访问
// vector_operator_bracket
#pragma once
#include "vector.h"
template <typename T>
T& Vector<T>::operator[](Rank r)
{
return _elem[r];
}
此后 对外的V[r]就对应于内部的V._elem[r]
insert 插入
所有后缀元素都右移一个单元 从而空出一个单元 插入
#pragma once
#include "vector.h"
template <typename T>
Rank Vector<T>::insert(Rank r, T const& e)
{
expand(); // 如有必要 扩容
for (int i = _size; i > r; i--) // 自后向前
_elem[i] = _elem[i - 1]; // 后继元素顺次后移一个单元
_elem[r] = e; // 置入新元素
_size++; // 更新容量
return r; // 返回秩
}
remove 删除
区间删除 将[lo,hi)区间中元素全删 并将后继全部前移
#pragma once
#include "vector.h"
// 区间删除
template <typename T>
Rank Vector<T>::remove(Rank lo, Rank hi)
{
if (lo == hi) return 0; // 为了效率单独处理退化情况
while (hi < _size)
_elem[lo++] = _elem[hi++]; // 自前向后 [lo,_size)顺次前移hi-lo
_size = lo; // 更新规模
shrink(); // 如有必要 缩容
}
// 单元素删除 可以看作区间删除的特例
template <typename T>
T Vector<T>::remove(Rank r)
{
T e = _elem[r]; // 备份被删除元素
remove(r, r + 1); // 调用区间删除算法
return e;
}
是否可以通过反复调用单元素删除来实现区间删除? 效率不高 删一个单元素 后继就要移动一次 对于每个元素都要这样做一次
find 无序查找
无序向量 T为可判等的基本类型 或者已经重载操作符==或!=
有序向量 T为可比较也可以判等的基本类型 或者已经重载操作符<或>
从hi出发 逆向地找 逐一地取出向量中的各个元素 与目标元素比对 不相等就忽略 如果到最后试图跃过lo 查找失败
// vector_find.h
#pragma once
#include "vector.h"
template <typename T>
Rank Vector<T>::find(T const& e, Rank lo, Rank hi) const
{
while ((lo < hi--) && (e != _elem[hi]));
return hi;
}
deduplicate 无序去重
每次遇到新元素 都在它的前驱中查找 find(x) 如果找到相同的 就剔除 没找到就保留 再去考察下一个元素 也就是直接后继
// vector_deduplicate.h
#pragma once
#include "vector.h"
template <typename T>
Rank Vector<T>::deduplicate()
{
int oldSize = _size;
Rank i = 1; // 从_elem[1]开始 而不是_elem[0]
while (i < _size) // 自前向后逐一遍历
find(_elem[i], 0, i) ? i++ : remove(i);
// _elem[i]是否和前缀[0,i)的元素有雷同? 若无雷同 考察后继 若有雷同 删除_elem[i]这一项
// 但做完remove(i)之后 现在的_elem[i]就是原来的_elem[i]的后继 不再需要i++
return oldSize - _size; // 向量规模变化量 即删除元素总数
}
traverse 遍历
统一对各元素分别实施visit操作 于是就有两种将visit操作传递到vector内部的方式
#pragma once
#include "vector.h"
#include <functional>
template <typename T>
void Vector<T>::traverse(std::function<void(T&)> visit) // 使用函数指针 只读或局部性修改
// std::function<void(T&)> func 就是接收T&参数的 返回void类型的 名为func的 函数指针
// 和void(*func)(T&)差不多
{
for (int i = 0; i < _size; i++)
visit(_elem[i]);
}
template <typename T> template <typename VST>
void Vector<T>::traverse(VST& visit) // 使用函数对象 全局性修改
{
for (int i = 0; i < _size; i++)
visit(_elem[i]);
}
对于函数对象 就可以这样写
template <typename T>
struct Increase
{
void operator()(T& e)
{
e++;
}
}
template <typename T>
void increase(Vector<T>& v)
{
v.traverse(Increase<T>());
}
disordered 逆序对个数
有序序列中任意一对相邻元素顺序
无序序列中总有一堆相邻元素逆序
相邻逆序对的数目 可以用来度量向量的逆序程度
// vector_disordered.h
#pragma once
#include "vector.h"
template <typename T>
Rank Vector<T>::disordered()
{
int n = 0; // 计数器
for (int i = 1; i < _size; i++) // 遍历各对相邻元素
n += (_elem[i - 1] > _elem[i]); // 逆序就计数
return n; // n=0 当且仅当向量有序
}
如果只需要判断是否有序 在首次遇到逆序对之后 就可以立即终止
把无序转化成有序 可以使后续操作更简单
uniquify 有序去重
有序向量中重复元素必定紧挨着构成一个区间 每个区间只要保留单个元素
// vector_uniquify.h
#pragma once
#include "vector.h"
template <typename T>
Rank Vector<T>::uniquify() // 单元素删除 低效版本
{
int oldSize = _size;
int i = 0;
while (i < _size - 1)
(_elem[i] == _elem[i + 1]) ? remove(i + 1) : i++;
return oldSize - _size;
}
对比一下无序的deduplicate是这样的
Rank i = 1;
while (i < _size)
find(_elem[i], 0, i) ? i++ : remove(i);
所以现在的uniquify就是 拿着一个 前驱里肯定没有任何重复元素 的元素 因为是有序的 所以只有首次出现的那个元素可以被保留 它之后的所有重复元素 都要被删除 所以i要从0开始
这个方法较为低效 因为重复的元素因为move操作 多次前移 如果直接将重复元素区间删除 会更高效
// vector_uniquify.h
#pragma once
#include "vector.h"
template <typename T>
Rank Vector<T>::uniquify() // 区间删除 高效版本
{
Rank i = 0, j = 0;
while (++j < _size)
{
if (_elem[i] != _elem[j])
_elem[++i] = _elem[j];
}
_size = ++i;
return j - i; // 向量规模变化量
}
i是重复元素首次出现的位置 j是向后扫描 如果j扫描到不再是重复元素了 而是新的元素首次出现了 i就+1 并直接把j扫描到的那个新元素复制到现在的这个_elem[i] 最后直接缩减向量的规模 也就是重新设置_size 不涉及任何显式的移动与删除操作
search 有序查找
// vector_search.h
template <typename T>
Rank Vector<T>::search(T const& e, Rank lo, Rank hi) const
{
return (rand() % 2) ?
binSearch_C(_elem, e, lo, hi) : fibSearch(_elem, e, lo, hi);
// 各有50%的概率选用二分查找C 或者 Fibonacci查找(略)
// 为什么是二分查找版本C 原因后面讲
}
search接口至少应该使有序向量自身的维护变得非常便利 让有序性得以延续
比如V.insert(1+V.search(e), e) 通过search寻找一个位置 然后插入 使得有序向量还是一个有序向量 即使查找失败 也要给新元素一个适当的插入位置 若有重复元素 也要按插入顺序有所排列 新插入的元素在最前或最后
约定 search接口的返回值 总是不大于目标e的最后一个元素的秩 如果有多个命中元素 返回秩最大的那个秩
若查找失败
-∞ < e < V[lo] 返回哨兵lo-1 这样后面插入时 就可以把元素放在lo的位置上
V[hi-1] < e < +∞ 返回hi-1 这样后面插入时 就可以把元素放在hi的位置上

如果有重复元素e 不大于e的最后一个元素 自然是这些元素的右端点 再在它的后面才插入e 正好符合约定
binSearch 二分查找
版本A
减而治之 以任一元素x = S[mi]为界 分成三部分 x称为轴点 总是取作中点

经过至多两次比较 或者命中或者问题规模变成一半
若e=x 命中 直接返回
若e
// vector_binSearch_A.h
#pragma once
#include "vector.h"
template <typename T>
static Rank binSearch_A(T const& e, Rank lo, Rank hi)
{
while (lo < hi)
{
Rank mi = (lo + hi) >> 1; // 取出lo和hi的中点
if (e < A[mi]) hi = mi; // 深入[lo,mi)
else if (A[mi] < e) lo = mi + 1; // 深入(mi,hi) 都是写的<号 建议总是写<号
else return mi; // 那实际上就是A[mi]=e 在mi命中
}
return -1; // 查找失败
}
二分查找A 进入左侧分支 只需要比较一次 但若要进入右侧分支 就要比较两次 不平衡
S.search(3,0,7)
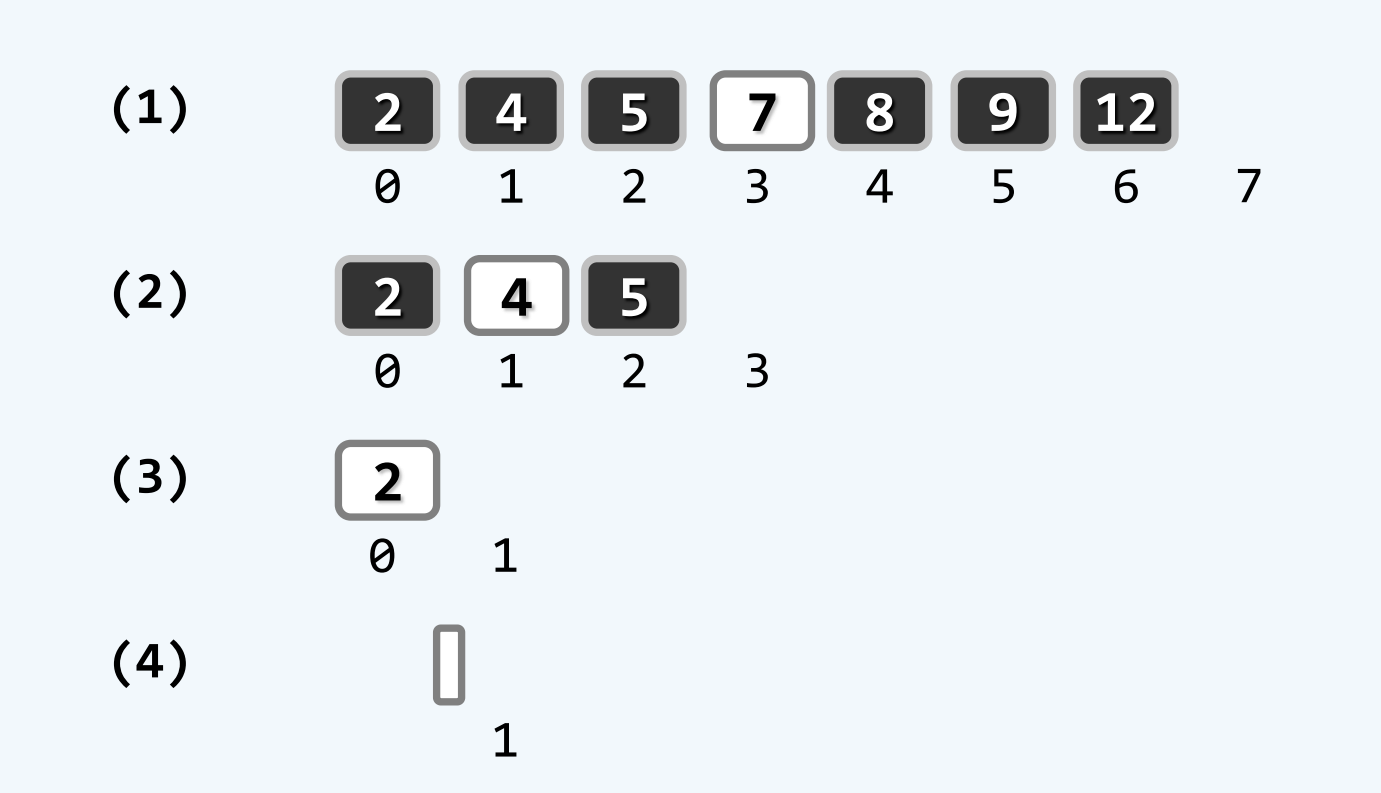
e=3
(1) 现在 lo=0 hi=7 mi=3 A[mi]=7 if 3<7? 是 进入左侧分支 hi=3
(2) 现在 lo=0 hi=3 mi=1 A[mi]=4 if 3<4? 是 进入左侧分支 hi=1
(3) 现在 lo=0 hi=1 mi=0 A[mi]=2 if 3<2? 否 if 2<3? 是 进入右侧分支 lo=1
(4) 现在 lo=1 hi=1 无法进入while循环 return -1 查找失败
版本B
二分查找A中 左右分支转向代价不平衡 希望无论向左向右都只需要一次比价 这样所有分支只有2个方向 而不是3个

取轴点mi为中点 e<x 深入[lo,mi) x<=e 深入[mi,hi) 其实只需要e<x? 比较一次 否则就深入右边 缺点是不能及时判断命中 只有hi-lo=1时 才能判断命中
// vector_binSearch_B.h
#pragma once
#include "vector.h"
template <typename T>
static Rank binSearch_B(T* A, T const& e, Rank lo, Rank hi)
{
while (1 < hi - lo) // 查找区间宽度为1时 算法才会终结
{
Rank mi = (lo + hi) >> 1;
(e < A[mi]) ? hi = mi : lo = mi; // [lo,mi)或[mi,hi)
}
return (e == A[0]) ? lo : -1; // 返回命中元素的秩 或者-1(失败)
}
但是二分查找A B都没有实现search()语义约定 没有返回不大于e的最后一个元素
版本C
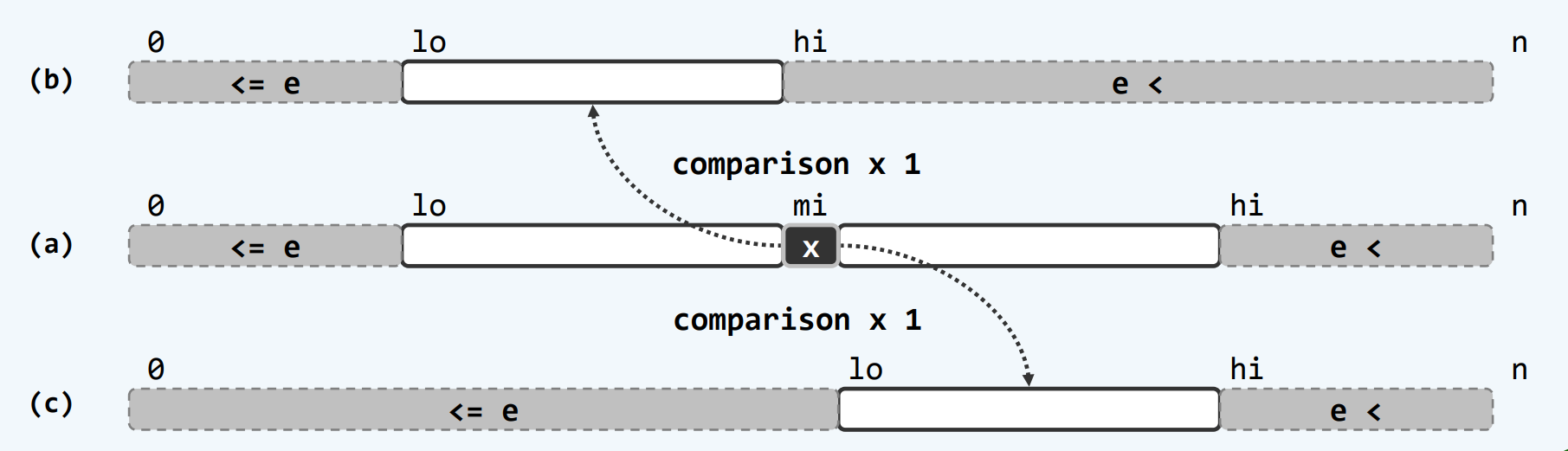
如果是从(a)到(b) 这个新的hi就等于mi 我们现在做的是有序查找 则A[mi]是[hi,n)中最小的 而e<A[mi]
如果是从(a)到(c) 这个新的lo-1就等于mi 有序查找 则A[mi]是[0,lo]中最大的 而A[mi]<=e lo=mi+1
则始终能保持A[0,lo) <= e < A[hi,n)
假如这种不变性可以一直保持 最后一定会hi=lo 而在[0,lo)的元素都是<=e 在[hi,n)的元素都是>e 那么就只要返回lo-1 这就是不大于e的最大元素
// vector_binSearch_C.h
#pragma once
#include "vector.h"
template <typename T>
static Rank binSearch_C(T* A, T const& e, Rank lo, Rank hi)
{
while (lo < hi)
{
Rank mi = (lo + hi) >> 1;
(e < A[mi]) ? hi = mi : lo = mi + 1;
}
return --lo; // lo-1 即不大于e的元素的秩 符合接口规定
}
比如 现在是1 3 5 7 9 我们要查找e=6
(1) lo=0 hi=4 mi=2 e=6<A[mi]=5? 否 则现在lo=mi+1=3 A[mi]是不大于e的 而区间是左闭区间 所以lo定位到mi的后继元素 移动区间的左侧 保证[lo,hi)中 区间内部的左侧不包含所有我们目前已知的不大于e的元素 因为我们最终的目标是找到最大的不大于e的元素 我们希望通过lo-1来得到这个元素 在本例中的这个时候 实际上e已经不在[lo,hi)之中了
(2) lo=3 hi=4 mi=3 e=6<A[mi]=7? 是 则现在hi=mi=3 A[mi]是大于e的 移动区间的右侧 保证[lo,hi)中 区间最右侧的元素是我们目前已知的最小的大于e的元素 但因为是右开区间 所以区间本身是不包含这个元素的 所以当lo=hi时 [lo,hi)收敛到的那个元素 当然这时候这个区间由于是右开区间 已经不可能包含任何元素了 一定是最小的大于e的元素 同时也是最大的不大于e的元素的后继元素 而我们要找到最大的不大于e的元素 就要lo-1
(3) lo=hi=3 不再是lo<hi 无法进入while循环 return –lo=2 A[2]=5 确实是最大的不大于e=6的元素
再比如 1 3 5 7 9 我们要查找e=5
(1) lo=0 hi=4 mi=2 e=5<A[mi]=5? 否 则现在lo=mi+1=3
(2) lo=3 hi=4 mi=3 e=5<A[mi]=7? 是 则现在hi=mi=3
(3) lo=hi=3 不再是lo<hi 无法进入while循环 return –lo=2 A[2]=5 确实是最大的不大于e=5的元素
在存在相等元素的时候也同样成立
bubbleSort 起泡排序
版本A 不是vector版本
依次比较每一对相邻元素 称为扫描 每次扫描称为一趟 发现有逆序的相邻元素 就交换它们 如果某一趟扫描没有发现相邻元素逆序 就结束扫描
void bubbbleSort(int A[], int n)
{
for(bool sorted = false; sorted=!sorted; n--)
for(int i=1; i<n; i++)
if(A[i-1] > A[i]) // 发生逆序
{
swap(A[i-1], A[i]); // 交换
sorted = false;
}
}
sorted=!sorted 是因为 如果上一次循环结束结果是sorted=false 将取反变为true 进入循环 如果上一次循环结果是sorted=true 取反变为false将退出循环 结束扫描
n-- 是因为每一趟交换之后 最大的元素必定在最后面 在下一轮扫描时 就不需要再扫描它了
最大的元素先就位 经k轮扫描交换之后 最大的k个元素必然就位 问题规模缩减至n-k 至多n趟扫描后 算法必然终止
版本B
版本A一趟扫描交换之后 右边一些元素必然是有序的 但左边未必无序 希望能尽早地判定 从而提前退出算法
每一趟扫描交换之前 都记录下此时是否存在逆序元素 如果存在 说明发生逆序的这对元素 其中起码有一个是恰在上一趟交换时 从别的地方换过来的 假如上一趟时这个逆序就存在 那么上一趟就应该能把它挑出来 不会遗留到这一趟 所以如果上一趟就没有逆序 没有发生交换 这一趟自然也不可能有逆序 不用发生交换 直接截断
// vector_bubbleSort_B.h
#pragma once
#include "vector.h"
template <typename T>
void Vector<T>::bubbleSort(Rank lo, Rank hi)
{
while (!bubble(lo, hi--););
// bubble返回的是有序标志 如果有序就停止循环 及时截断
}
template <typename T>
bool Vector<T>::bubble(Rank lo, Rank hi)
{
bool sorted = true; // 先认为有序 后面再逐个检查各对相邻元素
while (++lo < hi)
if (_elem[lo - 1] > _elem[lo])
{
sorted = false; // 整体尚未有序
swap(_elem[lo - 1], _elem[lo]); // 交换
}
return sorted; // 返回有序标志
}
版本C
∎∎∎∎ ∎∎∎∎∎∎∎∎∎∎∎∎∎
前缀 后缀
可能整个vector是这样的 只有前缀一小部分是乱序 后缀全都是有序的 就位的 需要排序的元素只聚集在很小的区间中 但是如果像我们之前那样扫描交换 后缀里的元素是不会发生调整顺序的 每趟扫描交换之后 都是前缀的最后一个、倒数第二个、倒数第三个元素逐渐就位
如果去记录上一趟扫描交换中所进行的最后一次交换的位置 这样就知道在上一趟的扫描交换中 有多长的后缀没有做过任何交换 那么只需要将hi直接指向新的最后交换的位置
// vector_bubbleSort_C.h
#pragma once
#include "vector.h"
template <typename T>
void Vector<T>::bubbleSort(Rank lo, Rank hi)
{
while (lo < (hi = bubble(lo, hi)));
}
template <typename T>
Rank Vector<T>::bubble(Rank lo, Rank hi)
{
Rank last = lo; // 记录最右侧逆序对位置
while (++lo < hi) // 自左向右
if (_elem[lo - 1] > _elem[lo]) // 若逆序
{
last = lo; // 更新最右侧逆序对位置记录
swap(_elem[lo - 1], _elem[lo]);
}
return last; // 返回最右侧逆序对位置 而不再是bool型sorted
}
算法的稳定性
输入重复元素之后 输出序列中 重复元素的相对次序不发生改变 则算法是稳定的 bubbleSort中 重复的元素a和b相对位置想要发生变化是不可能的 它们肯定是要先作为相邻元素才可能发生交换 但是元素相同是不可能发生交换的 所以bubbleSort是一个稳定的算法
mergeSort 归并排序

先将序列一分为二 将子序列递归排序 再合并有序子序列
二路归并

这是两个已经排好序的两段 要把它们归并 只关注首元素 从首元素中挑出更小的元素 如果相等就任意取一个 取出后 后续元素补位
在归并排序中 参与二路归并的两个序列 其实是S[lo,hi)=S[lo,mi)+S[mi,hi) A=B+C 来自于同一个更大的向量
版本A
// vector_mergeSort.h
#pragma once
#include "vector.h"
template <typename T>
void Vector<T>::mergeSort(Rank lo, Rank hi)
{
if (hi - lo < 2) return; // 单元素区间有序
int mi = (lo + hi) >> 1; // 以中点为界
mergeSort(lo, mi); // 对前半段排序
mergeSort(mi, hi); // 对后半段排序
merge(lo, mi, hi); // 归并
}
template <typename T>
void Vector<T>::merge(Rank lo, Rank mi, Rank hi)
{
// A = B + C
T* A = _elem + lo; // 合并后的向量A[0,hi-lo]=_elem[lo,hi]
int lb = mi - lo;
T* B = new T[lb]; // 前子向量B[0,lb)=_elem[lo,mi)
for (Rank i = 0; i < lb; B[i] = A[i++]);
// 为B开辟新的内存空间 并将A的前半部分复制到前子向量B
int lc = hi - mi;
T* C = _elem + mi; // 后子向量C[0,lc)=_elem[mi,hi)
// C现在就是A的后半段 只是用了一个新的指针去索引
// 没有开辟新的内存 也没有复制
for (Rank i = 0, j = 0, k = 0;(j < lb) || (k < lc);)
// B[j] C[k]都没了 算法就退出
{
if ((j < lb) && (lc <= k) || (B[j] <= C[k]))
// && 的优先级比 || 更高 就相当于 ( (j < lb) && (lc <= k) ) || (B[j] <= C[k])
// (B[j]有值 并且 C[k]已经没有了) 或者 C[k]大于等于B[j]
A[i++] = B[j++]; // 就是取两边相比之下数值更小的 或者只有一边还剩下了元素
// 这里是B的元素更小 所以取B中的元素放到A里
if ((k < lc) && (lb <= j) || (c[k] <= B[j]))
// (C[k]有值 并且 B[j]已经没有了) 或者 B[j]大于等于C[k]
A[i++] = C[k++]; // 取C中的元素放到A里
}
delete[] B; // 释放临时空间B
}
其实A最后是被覆盖的 B是A的前半段 已经从A复制过来了 不怕被覆盖 C是后半段 但是A被覆盖的部分决不会覆盖掉C还未处理的地方
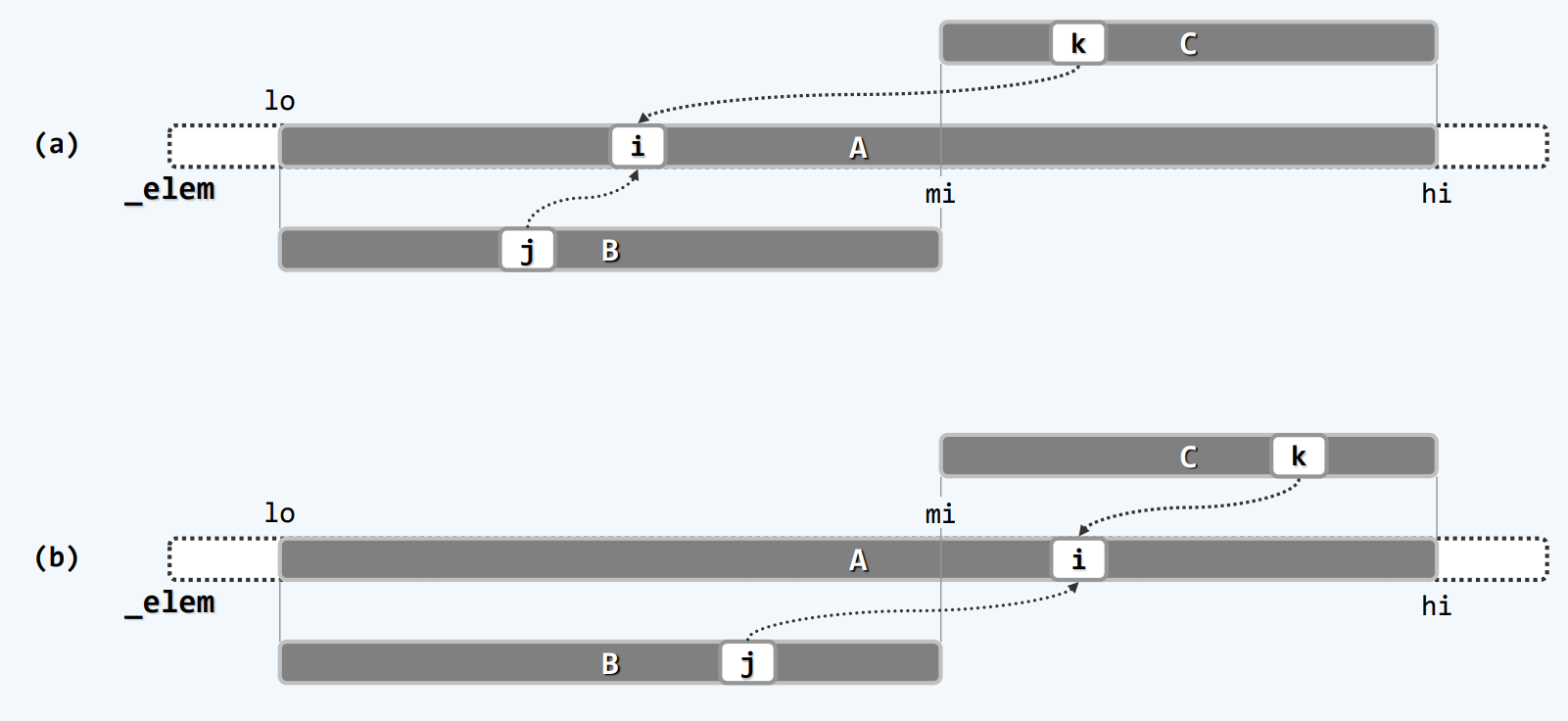
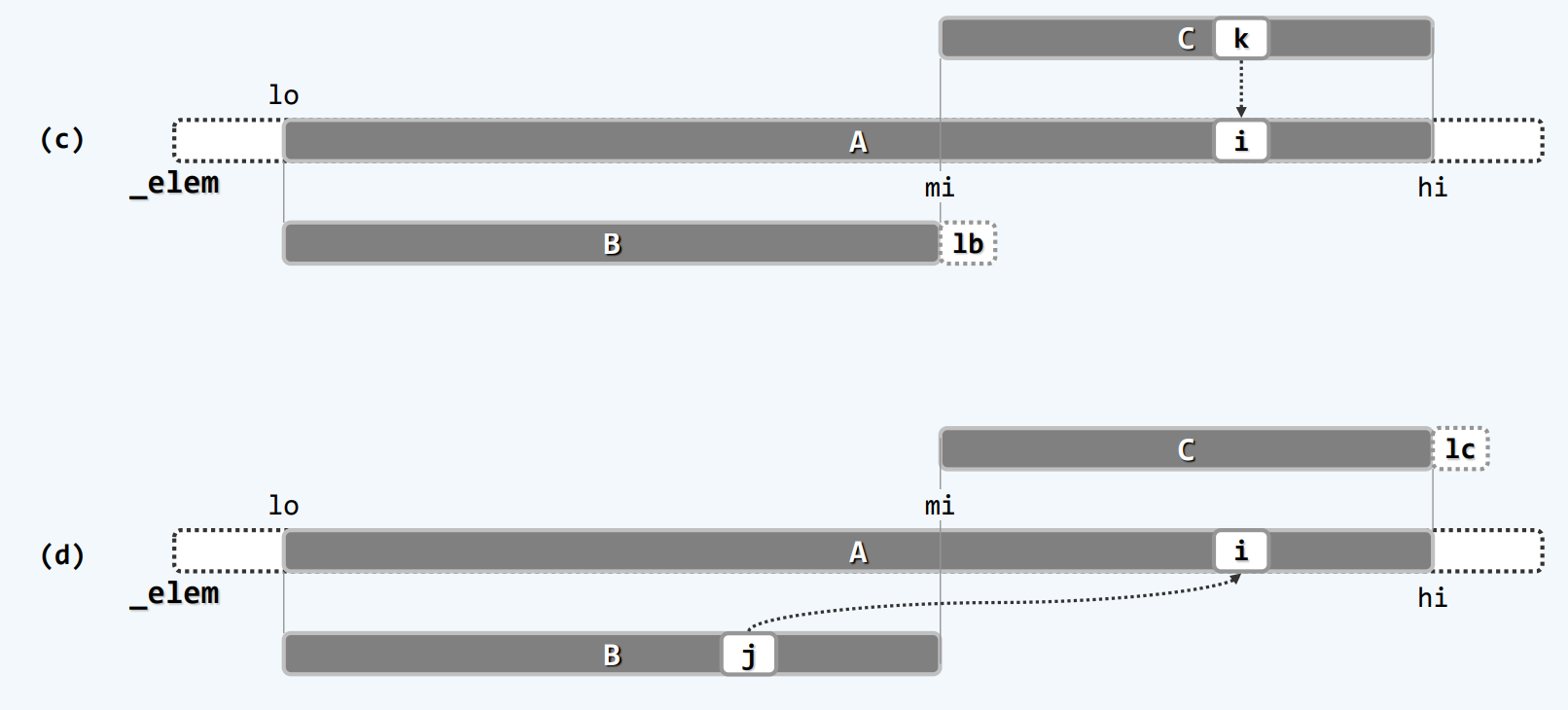
现在是C不复制 省时间 A不开辟 省空间
我自己想的就是拙劣的空间换时间 直接开辟hi-lo长度的空向量 然后在原向量的前半段和后半段分别遍历比较 挑选出来元素之后 就复制到新开辟的这个向量里 但是这样的话 新开辟的这个向量的地址并不是_elem+lo
B和C的地位是不对等的 B是复制过来的 而C就是A的一部分 B耗尽时 如图(c) 此时对于C尾部元素的转移是多余的 因为它们本来就在那
版本B 删除冗余逻辑
// vector_mergeSort.h
template <typename T>
void Vector<T>::merge(Rank lo, Rank mi, Rank hi)
{
T* A = _elem + lo;
int lb = mi - lo;
T* B = new T[lb];
for (Rank i = 0; i < lb; B[i] = A[i++]);
int lc = hi - mi;
T* C = _elem + mi;
for (Rank i = 0, j = 0, k = 0;(j < lb);) // 删除了 || (k < lc) 因为不需要考虑C提前耗尽 只要B提前耗尽 就终止这个算法
{
// 两个if语句相较上个版本 交换了位置
if ((k < lc) && (c[k] <= B[j])) // 进入循环时已经判断了j<lb 则不想需要再考虑j与lb
A[i++] = C[k++];
if ((lc <= k) || (B[j] <= C[k]))
A[i++] = B[j++];
}
delete[] B;
}
list
- 根据是否修改数据结构 所有操作大致分为两类方式
- 静态 仅读取 数据结构的内容及组成 一般不变 get search
- 动态 需写入 数据结构的局部或整体将改变 insert remove
- 数据元素的存储与组织方式也分为两种
- 静态 数据空间整体创建或销毁 数据元素的物理存储次序 与其逻辑次序严格一致 可支持高效的静态操作
比如vector的get search 但对于动态操作 insert 需要把后继全部后移 - 动态 各数据元素的物理空间 在生命期内是动态地 逐步地分配
- 静态 数据空间整体创建或销毁 数据元素的物理存储次序 与其逻辑次序严格一致 可支持高效的静态操作
列表list采用动态存储策略 其中元素称为节点node 物理上没有规律 各节点通过指针或引用彼此联接 在逻辑上构成一个线性序列
 相邻节点互称为前驱predecessor 后继successor
相邻节点互称为前驱predecessor 后继successor
除了第一个节点 其余节点都有唯一的前驱 首节点first front
除了最后一个节点 其余节点都有唯一的后继 末节点 last rear
向量支持o(1)的循秩访问 v[i]的物理地址=v + i×s s是单个单元占用的空间量
列表也是线性结构 它应该也可以用秩定位节点 从头到尾端出发 从头/尾端出发 沿后继/前驱引用 但是顺序存取list 循位置访问 访问成本过高 访问第i个元素就要利用节点之间的相互引用 找到特定的节点 o(n)
模仿向量循秩访问方式 重载下标操作符 效率比较低
// list_operator_bracket.h
#pragma once
#include "list.h"
template <typename T>
ListNodePosi<T> List<T>::operator[](Rank r) const
{
ListNodePosi<T> p = first(); // 从首节点出发
while (0 < r--) p = p->succ; // 不断沿着succ引用向后行进 结束时p正好处于秩为r的节点
return p->data;
}
ListNode 列表节点
// listNode.h
#pragma once
using Rank = unsigned int; //秩
template <typename T> struct ListNode;
template <typename T> using ListNodePosi = ListNode<T>*; //列表节点位置
template <typename T> struct ListNode
{
T data; // 数值
ListNodePosi<T> pred; // 前驱
ListNodePosi<T> succ; // 后继
ListNode() {} // 针对header和trailer的构造
ListNode(T e, ListNodePosi<T> p = NULL, ListNodePosi<T> s = NULL)
: data, pred(p), succ(s) {} // 默认构造器
ListNodePosi<T> insertAsPred(T const& e); // 前插入
ListNodePosi<T> insertAsSucc(T const& e); // 后插入
};
list模板类


header和trailer 是与生俱来的 二者并不相同
first和last 并不见得不相同 甚至不能保证它们存在
对外 first和last是可见的 header和trailer不可见
// list.h
#pragma once
#include "listNode.h"
template <typename T>
class List
{
private:
int _size; // 规模
ListNodePosi<T> header;
ListNodePosi<T> trailer; // 头尾哨兵
protected:
void init(); //列表创建时的初始化
Rank clear(); //清除所有节点
void copyNodes(ListNodePosi<T>, Rank); //复制列表中自位置p起的n项
ListNodePosi<T> merge(ListNodePosi<T>, Rank, List<T>&, ListNodePosi<T>, Rank); //归并
void mergeSort(ListNodePosi<T>&, Rank); //对从p开始连续的n个节点归并排序
void selectionSort(ListNodePosi<T>, Rank); //对从p开始连续的n个节点选择排序
void insertionSort(ListNodePosi<T>, Rank); //对从p开始连续的n个节点插入排序
void radixSort(ListNodePosi<T>, Rank); //对从p开始连续的n个节点基数排序
public:
// 构造方法
List() { init(); } //默认
List(List<T> const& L) { copyNodes(L.first(), L._size); } //整体复制列表L
List(List<T> const& L, Rank r, Rank n) //复制列表L中自第r项起的n项
{
ListNodePosi<T> p = L.first();
while (0 < r--) p = p->succ;
copyNodes(p, n);
}
List(ListNodePosi<T> p, Rank n) { copyNodes(p, n); } //复制列表中自位置p起的n项
// 析构方法
~List() { clear(); delete head; delete tail; } //释放(包含头、尾哨兵在内的)所有节点
// 只读访问接口
Rank size() const { return _size; } //规模
bool empty() const { return _size <= 0; } //判空
ListNodePosi<T> operator[](Rank r) const; //重载,支持循秩访问(效率低)
ListNodePosi<T> first() const { return header->succ; } //首节点位置
ListNodePosi<T> last() const { return trailer->pred; } //末节点位置
bool valid(ListNodePosi<T> p) //判断位置p是否对外合法
{
return p && (trailer != p) && (head != p);
} //将头、尾节点等同于NULL
ListNodePosi<T> find(T const& e) const //无序列表查找
{
return find(e, _size, trailer);
}
ListNodePosi<T> find(T const& e, Rank n, ListNodePosi<T> p) const; //无序区间查找
ListNodePosi<T> search(T const& e) const //有序列表查找
{
return search(e, _size, trailer);
}
ListNodePosi<T> search(T const& e, Rank n, ListNodePosi<T> p) const; //有序区间查找
ListNodePosi<T> selectMax(ListNodePosi<T> p, Rank n); //在p及其n-1个后继中选出最大者
ListNodePosi<T> selectMax() { return selectMax(header->succ, _size); } //整体最大者
// 可写访问接口
ListNodePosi<T> insertFirst(T const& e); //将e当作首节点插入
ListNodePosi<T> insertLast(T const& e); //将e当作末节点插入
ListNodePosi<T> List<T>::insertBefore(ListNodePosi<T> p, T const& e); // 前插入 后插入完全对称
ListNodePosi<T> insert(ListNodePosi<T> p, T const& e); //将e当作p的后继插入
ListNodePosi<T> insert(T const& e, ListNodePosi<T> p); //将e当作p的前驱插入
T remove(ListNodePosi<T> p); //删除合法位置p处的节点,返回被删除节点
void merge(List<T>& L) { merge(header->succ, _size, L, L.header->succ, L._size); } //全列表归并
void sort(ListNodePosi<T>, Rank); //列表区间排序
void sort() { sort(first(), _size); } //列表整体排序
Rank deduplicate(); //无序去重
Rank uniquify(); //有序去重
// 遍历
void traverse(void (*)(T&)); //依次实施visit操作(函数指针)
template <typename VST> void traverse(VST&); //依次实施visit操作(函数对象)
};
构造
// list_init.h
#pragma once
#include "list.h"
template <typename T>
void List<T>::init()
{
header = new ListNode<T>;
trailer = new ListNode<T>;
header->succ = trailer; header->pred = NULL;
trailer->pred = header; trailer->succ = NULL;
_size = 0;
}
现在 对外可见的那个列表是空的 first与last之间的才对外可见
insertBefore 前插入
#pragma once
#include "list.h"
template <typename T>
ListNodePosi<T> List<T>::insertBefore(ListNodePosi<T> p, T const& e)
{
_size++;
return p->insertAsPred(e);
}
template <typename T>
ListNodePosi<T> ListNode<T>::insertAsPred(T const& e)
{
ListNodePosi<T> x = new ListNode(e, pred, this);
// (b)创建节点 数值为e 新插入节点的前驱是当前的前驱 p->pred 新插入节点的后继是当前节点this 也就是p
pred->succ = x; // (c)原来的前驱 以新的节点作为后继
pred = x; // 当前节点 以新的节点作为前驱
return x;
}
注意到调用时使用的是p->insertAsPred(e) 使用的是-> 并不是. 因为p是ListNodePosi<T> 是一个指针 不是对象 不能调用方法
(*p).insertAsPred(e)和p->insertAsPred(e) 是等效的
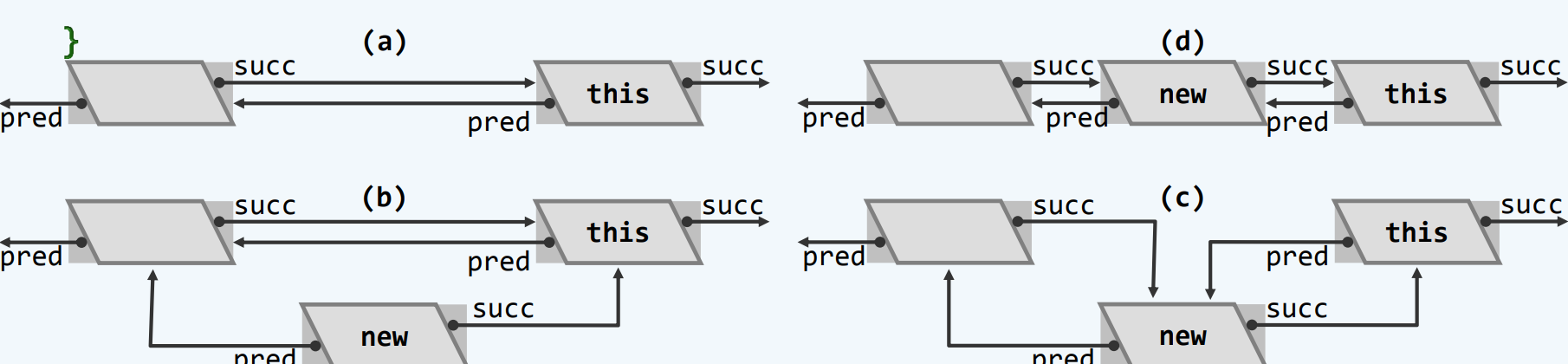
即使this是首节点也没问题 因为有头哨兵
该算法在局部进行 只涉及到3个节点 复杂度为常数
copyNodes 基于复制的构造
// list_copyNodes.h
#pragma once
#include "list.h"
template <typename T>
void List<T>::copyNodes(ListNodePosi<T> p, Rank n) // 从某一个列表的位置p开始 随后的连续n个节点
{
init(); // 创建空列表 创建头尾哨兵 并做初始化
while (n--)
{
insertBefore(trailer, p->data); // 把 从位置p开始的n项 依次作为末节点插入
p = p->succ; // 转向当前节点的后继
}
}
remove 删除
// list_remove.h
#pragma once
#include "list.h"
template <typename T>
T List<T>::remove(ListNodePosi<T> p) // 删除位置p处的节点 并返回其数值
{
T e = p->data;
p->pred->succ = p->data; // 把p现在的后继 当作p现在的前驱的后继
p->succ->pred = p->pred;
delete p;
_size--;
return e; // 返回数值
}
clear 析构
// list_clear.h
#pragma once
#include "list.h"
template <typename T>
Rank List<T>::clear()
{
int oldSize = _size;
while (0 < _size)
remove(header->succ); // 反复删除首节点 直到列表变空 对外可见的节点有多少个 就删除多少次
return oldSize;
}
find 无序查找
以位置为p的某个特定节点为基准 在它的n个真前驱(不包括它自己)中 找到某个可能存在的数值为特定值e的节点 找到等于e的最后者
// list_find.h
#pragma once
#include "list.h"
template <typename T>
ListNodePosi<T> List<T>::find(T const& e, Rank n, ListNodePosi<T> p) const
{
while (0 < n--)
if (e == (p = p->pred)->data) // 从后往前 取出数据与e比对 直到命中或范围越界
return p;
return NULL; // 越出左边界 查找失败
}
find(e,n,p) 这个字母顺序 很容易就知道是p的n个真前驱 如果重载成find(e,p,n) 就是在p的n个真后继里寻找
deduplicate 无序去重
// list_deduplicate.h
#pragma once
#include "list.h"
template <typename T>
Rank List<T>::deduplicate()
{
if (_size < 2)
return 0;
Rank oldSize = _size;
ListNodePosi<T> p = first(); // p从首节点开始
Rank r = 1;
while (trailer != (p = p->succ))
{
ListNodePosi<T> q = find(p->data, r, p); // 在p的n个真前驱中 查找重复
q ? remove(q) : r++; // 若真的存在 删除它 删完之后 r不用增加1 p也归入前缀了 否则秩递增 p就归入前缀了
}
return oldSize - _size;
}
但是q与p相同 为什么倾向于删除q? 因为删除p是麻烦的 会使while里p=p->succ存在风险
uniquify 有序唯一化
// list_uniquify.h
#pragma once
#include "list.h"
template <typename T>
Rank List<T>::uniquify() // 成批剔除重复元素
{
if (_size < 2) return 0; // 平凡列表自然没有重复
Rank oldSize = _size;
ListNodePosi<T> p = first();
ListNodePosi<T> q;
while (trailer != ( q = p->succ)) // 反复考察紧邻的节点对(p,q)
{
if (p->data != q->data)
p = q; // 若互异 则转向下一区段
else
remove(q); // 若雷同 删除后者
}
return oldSize - _size;
}
只需遍历整个列表一趟
search 有序查找
在p的n个真前驱中 找到不大于e的最后者
// list_search.h
#pragma once
#include "list.h"
template <typename T>
ListNodePosi<T> List<T>::search(T const& e, Rank n, ListNodePosi<T> p) const
{
while (0 <= n--)
if (((p = p->pred)->data) <= e) // 从后往前 转向p的直接前驱 取出数据与e比较
break;
return p;
}
有序查找相比无序查找 根本没有提升效率 这是因为列表是循位置访问
selectionSort 选择排序
每次在篮子中找到最大的 将它转移出来
bubbleSort也是selectionSort 扫描交换其实是从当前最大的元素开始 然后往后和邻居交换 直到队伍末尾 相邻位置比较后就发生交换 元素移动操作太多 还不如一口气比较 然后一步到位地到达队伍末尾
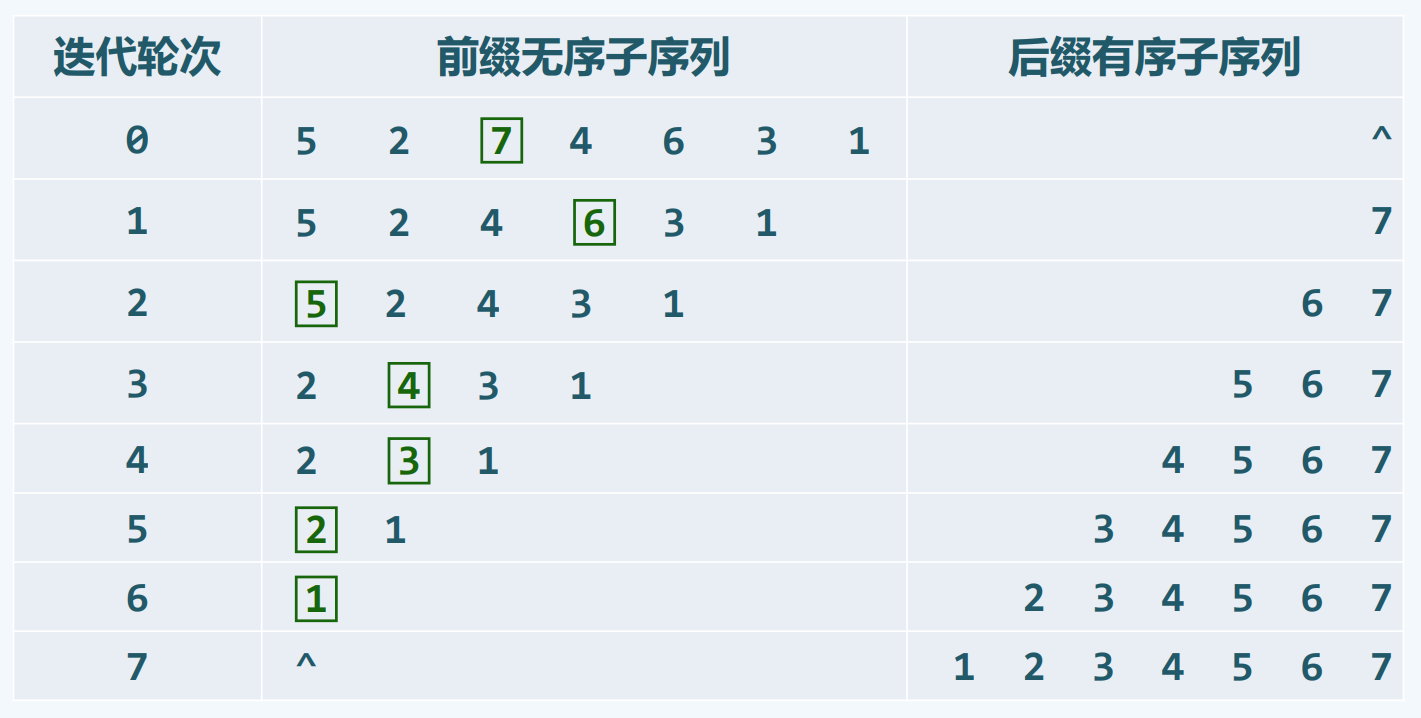
其实前缀序列和后缀序列是连着的 每次迭代只做了1次元素的移动 当前最大元素挪到最 末端 列表这种只靠引用的非常容易挪动 改变引用或者直接交换数据都可以
// list_selectionSort.h
#pragma once
#include "list.h"
template <typename T>
void List<T>::selectionSort(ListNodePosi<T> p, Rank n)
{
ListNodePosi<T> head = p->pred;
ListNodePosi<T> tail = p;
// 待排序区间
for (int i = 0; i < n; i++)
tail = tail->succ;
while (1 < n)
{
insertBefore(tail, remove(selectMax(head->succ, n))); //找到最大的值 删掉 然后把remove返回的这个值 插入到tail之前
tail = tail->pred; // tail每次向前移动一个节点 tail是待排列序列的尾部
n--;
}
}
// list_selectMax.h
#pragma once
#include "list.h"
template <typename T>
ListNodePosi<T> List<T>::selectMax(ListNodePosi<T> p, Rank n)
{
ListNode<T> max = p; // 记录当前最大节点
for (ListNode<T> cur = p; 1 < n; n--) // cur是当前遍历
if (!lt((cur = cur->succ)->data, max->data))
// !lt less than 不小于 前者不小于后者 就把max更新为这个不小的
// 若有重复的 最终它会选取最靠后的 那么max只可能递增 不会下降
// gt greater than
max = cur;
return max;
}
insertBefore(tail, remove(selectMax(head->succ, n)));
insert里用了new remove里用了delete
虽然可以认为是常数时间 但它们用时是通常基本操作的100倍
其实只要修改部分节点的引用就可以 或者把最大的数据交换到队末
[p,p+n) 从首节点逐一比对 记录下当前最大的元素 总感觉可以二分地比对 但是列表用不了二分
insertSort 插入排序
整理扑克牌 抽到就放中间 将更小的牌向左移动 空出位置 将新收到的牌插入
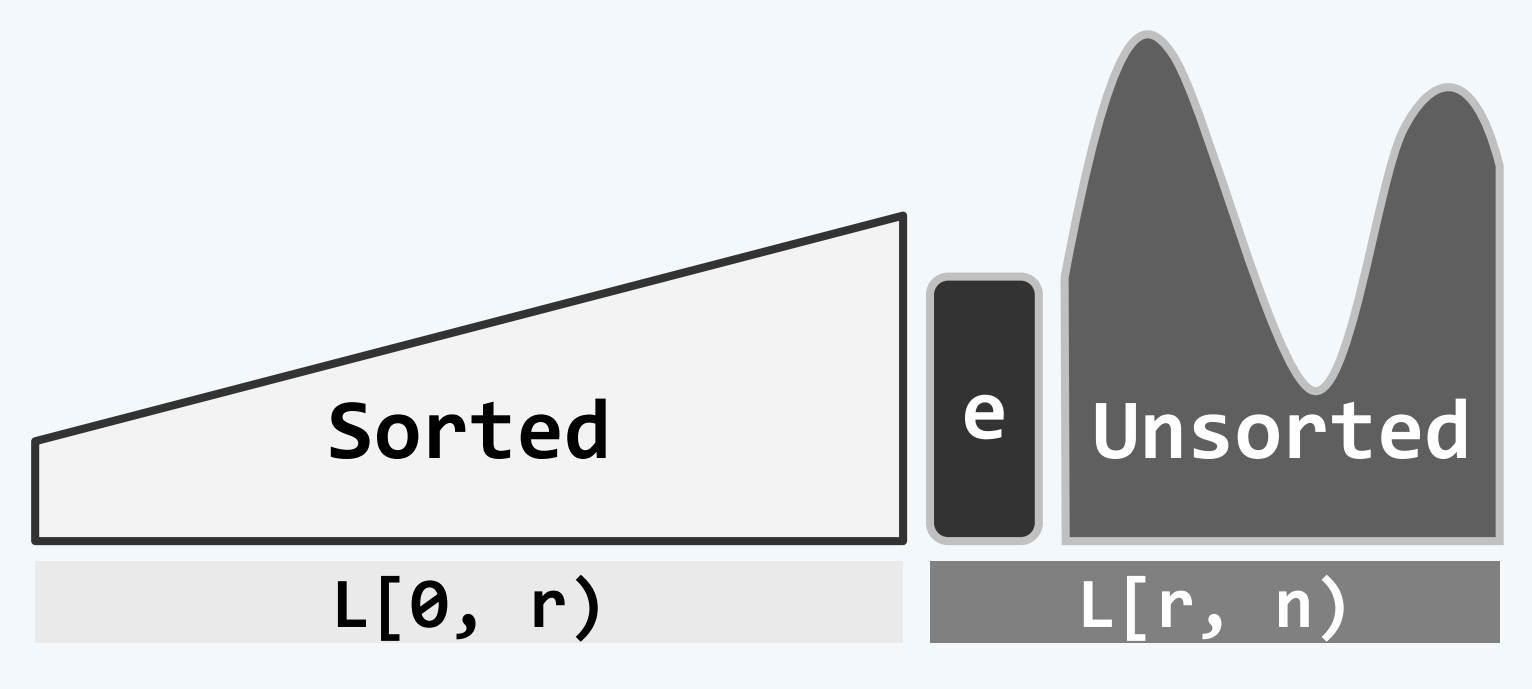
初始时 sorted长度为0 将新收到的牌 插入到已有的牌中 将e插入sorted
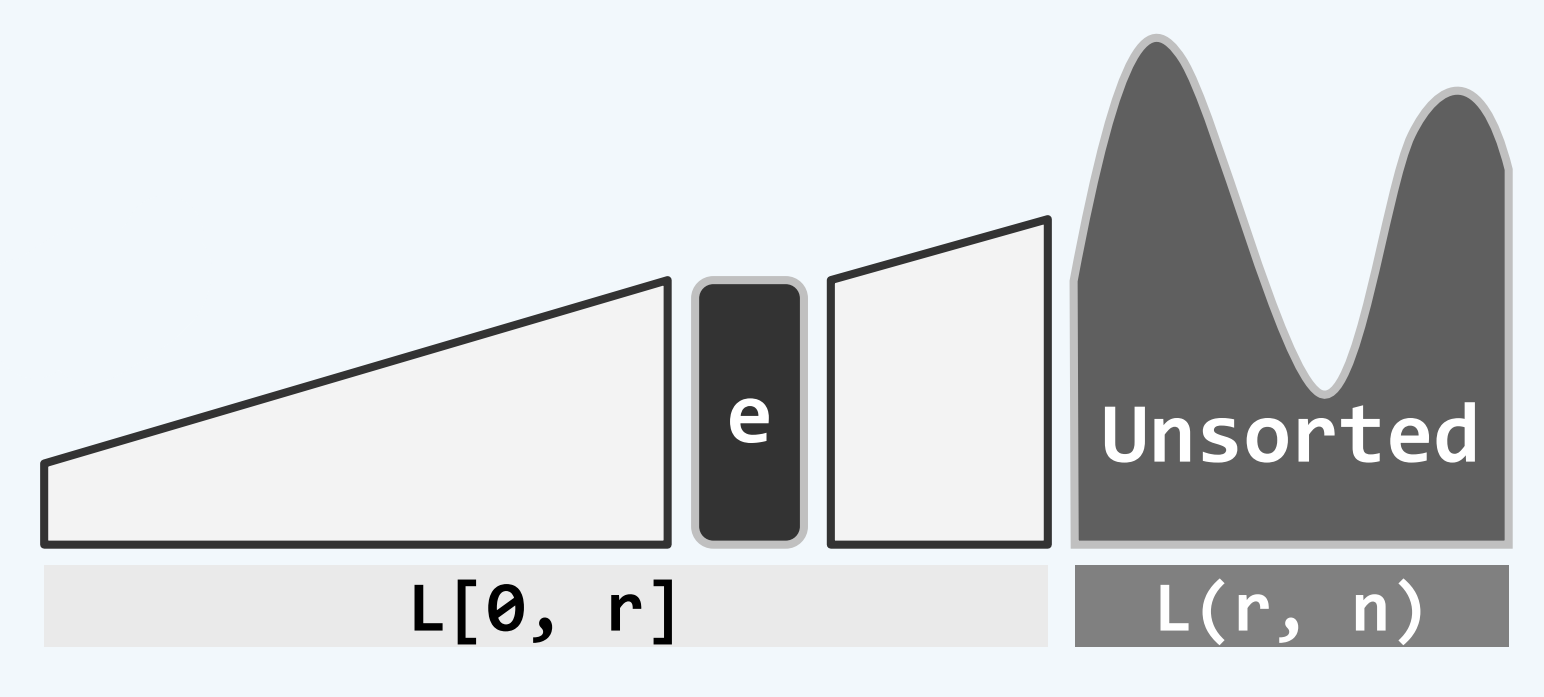
可以发现从L[0,r) L[r,n)变成L[0,r] L(r,n)了 开闭区间发生变化
selectionSort是后缀无序 前缀有序 从无序中挑出最大的 放在有序那堆里 无序中所有元素都不能超过有序的最小值
insertSort是前缀有序 后缀无序 为新来的元素在有序中找到一个位置 使有序仍保持有序 但不限定无序中的元素 因为它和有序没关系

// list_insertSort.h
#pragma once
#include "list.h"
template <typename T>
void List<T>::insertionSort(ListNodePosi<T> p, Rank n)
{
for (int r = 0; r < n; r++) // r是已经排序的前缀长度
{
insertAfter(search(p->data, r, p), p->data); // search返回一个不大于新拿到的牌的最靠后的那张牌
p = p->succ; // p是未排序的后缀的开头 最新拿到的那张牌 在有哨兵时 p->succ永远是安全的
remove(p->pred);
}
}
在已经有序的序列中查找 为什么不用二分查找?在选择排序找最大值时 也联想到了二分查找 那么为了用binSearch 直接舍弃List 而用Vector? 查找一定会加快 但insert remove都很慢 比如insert要把所有后继都往后移 而不是像List一样只要修改局部的引用
stack queue
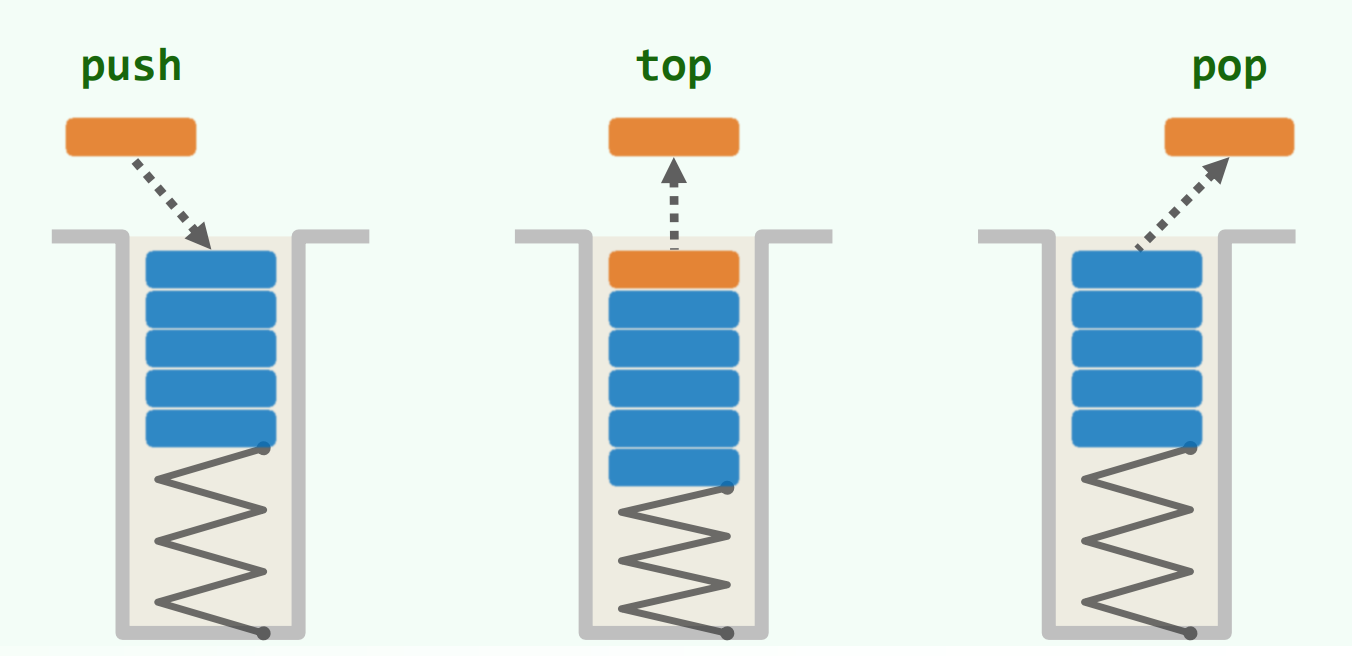
栈底bottom 栈顶top LIFO 后进先出
站属于线性序列的特例 所以可以基于向量或列表派生
// stack.h
#pragma once
#include "../vector/vector.h"
template <typename T>
class Stack : public Vector<T> // 使用public就可以直接沿用size() empty()等
{
public:
void push(T const& e) { insert(e); } // 入栈
T pop() { return remove(size() - 1); } // 出战
T& top() { return (*this)[size() - 1]; } // 取栈顶 返回当前向量的末元素
// 都可以写成this->insert(e) this->size()
};
逆序输出:进制转换
| 商 10进制转换为2进制 | 余数 | 商 10进制转换为5进制 | 余数 |
|---|---|---|---|
| 89 | 1 | 2013 | 3 |
| 44 | 0 | 402 | 2 |
| 22 | 0 | 80 | 0 |
| 11 | 1 | 16 | 1 |
| 5 | 1 | 3 | 3 |
| 1 | 1 | 0 | |
| 0 | |||
| 结果为:1011001 | 结果为:31023 |
只要自底向上输出 但计算过程是自下而上
栈 每计算得到1个数位 就将它压入栈中 输出时优先输出栈顶元素
// stack_convert.h
#include "stack.h"
void convert(Stack<char>& S, __int64 n, int base)
{
static char digit[] = { '0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F' };
while (n > 0)
{
S.push(digit[n % base]); // 余数入栈
n /= base; // n更新为其对base的除商
}
}
int main()
{
Stack<char> S;
__int64 n = 89;
int base = 2;
convert(S, n, base); // 用栈记录转换得到的各数位
while (!S.empty())
printf("%c", S.pop()); // 逆序输出
}
递归嵌套:括号匹配

0)平凡 无括号自然匹配
1)减而治之 ----E----匹配 则(----E----)一定匹配
反过来不一定成立 比如( ()())( )匹配 但去掉外层括号的()())(不匹配
2)分而治之 ----E----和----F----匹配 则----E--------F----一定匹配
反过来不一定成立 比如(() ())()是匹配的 但分开为(()和())() 这两个都是不匹配的
消去一对紧邻的左右括号 而不是(----E----)两边的括号
----L----()----R----匹配 当且仅当 ----L--------R----匹配
但怎样找到这样的括号?
可以线性扫描直到找到这对括号 将它删除 但难道接下来还要再一次从头开始扫描再找吗

遇到左括号就入栈 再遇到右括号 不仅右括号不入栈 栈顶的左括号也要弹出 等效于刚才被删除的括号 从未存在过 实际上只需要记录左括号
// stack_paren.cpp
#include "stack.h"
bool paren(const char exp[], int lo, int hi)
{
Stack<char> S; // 使用栈记录已发现但尚未匹配的左括号
for (int i = lo; i < hi; i++) // 逐一检查当前字符
{
if ('(' == exp[i]) // 是左括号
S.push(exp[i]); // 左括号入栈
else if (!S.empty()) // 否则就是右括号
S.pop(); // 否则就是右括号 遇右括号时 如果栈非空 弹出栈顶的左括号
else
return false; // 否则栈为空 即遇到右括号时 栈为空 必然不匹配
}
return S.empty(); // 栈空当且仅当匹配 若非空 必定是有左括号 但没有右括号和它配对
}

为什么要用栈? 只要用一个整数计数器就可以完成任务 遇到(就加1 遇到)就减1 若追钟回到0 即匹配 实际上这个数字正是栈当前的规模 但是栈可以推广至多种括号并存的情况
多括号并存

左括号 无论什么括号 都入栈
右括号 栈顶左括号若与它配对 出栈 否则失配
只要能定义是否匹配的规则 不一定是必须括号匹配
栈混洗
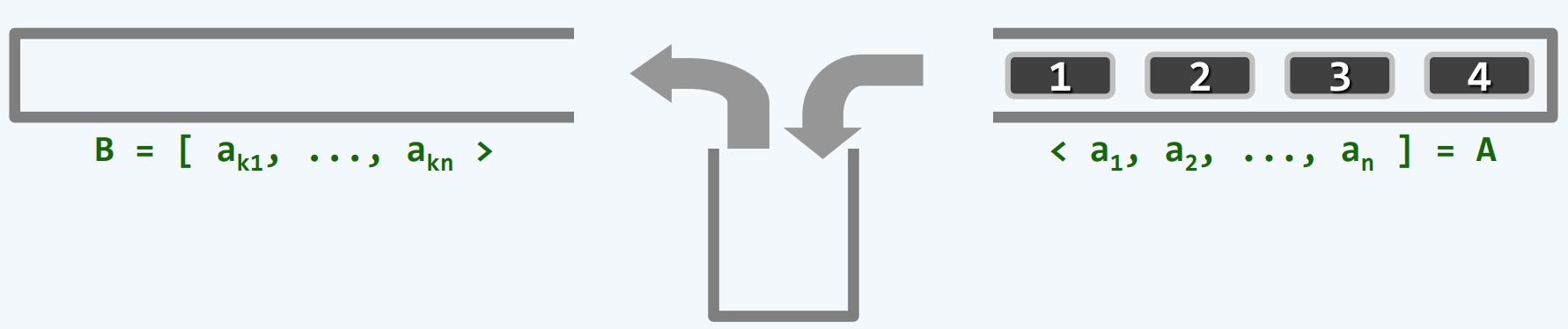
按照某种规则 对栈中元素重新排列
最初 <a1, a2, ..., an] = A, B=∅, S=∅
元素都存在于栈A中 要用某种方式转移到另一个初始为空的栈B中 为此需要借助一个中转栈S
只允许将A的顶元素弹出并压入S 或者将S的顶元素弹出并压入B
经过一系列操作 A中元素全部转入B中
B = [ak1, ..., akn> 称为A的一个栈混洗
同一输入序列 可以有多种栈混洗 只取决于A push进S 与 pop到B的顺序
可能的栈混洗总数 不可能超过全排列n!
中缀表达式
在表达式中寻找能优先计算的子串 算完把数值放在原来位置上 减而治之 最终将消除掉所有运算符 但很难定位到当前可以计算的运算符 使用线性扫描 扫到运算符也不能确认它是当前可计算的 将扫描过的部分保存成栈 能局部计算的部分 和不能计算的缓冲 逐步将尚未扫描的部分扫描处理掉

1)是数字就进栈 运算符在尚未判定它有足够高的运算符优先级时也进栈
2)算到4+2×3时 遇到减号 相对于现在靠近顶端的乘号 优先级更低 所以现在乘号可以计算了 并将计算结果放入栈中 于是变成4+6
3)遇到减号 减号和加号优先级相当 但加号出现在前 先算 就变成10-
4)先遇到1 又遇到0 两个数字挨着 这是一个多位数 那么就需要是把1乘上10之后 再加上新来的数字0 1×10+0=10 重新放入栈中 就变成了10-10
5)遇到除号 除法优先级高 则减法达不到执行的时候 于是变成10-10/5
6)遇到\0 看到了末尾标志 那么所有运算符都可以进行计算了 最后栈内的唯一元素 就是我们要的结果
每次计算时 2×3 10/5都不是那么自然
// stack_evaluate.cpp
#include "stack.h"
#include <cctype>
float evaluate(char* S, char*& RPN)
{
Stack<float> opnd; // 运算数栈
Stack<char> optr; // 运算符栈
optr.push('\0'); // 结束标志首先推入操作符栈
while (!optr.empty()) // 逐渐处理各字符 直至运算符空
{
if (isdigit(*S)) // 当前字符如果是数字
readNumber(S, opnd); // 读入数字 放入运算符栈 可能多位要完整读入 具体实现暂略
else // 当前字符是运算符
switch (orderBetween(optr.top(), *S))
{
// 查要看其与栈顶运算符之间优先级的高低
// 暂略
}
}
return opnd.pop();
}
优先级表
#define N_OPTR 9 // 定义运算符的数量,用于优先级矩阵的维度
const char pri[N_OPTR][N_OPTR] = // 运算符优先级[栈顶][当前]
{
'>', '>', '<', '<', '<', '<', '<', '>', '>',
'>', '>', '<', '<', '<', '<', '<', '>', '>',
'>', '>', '>', '>', '<', '<', '<', '>', '>',
'>', '>', '>', '>', '<', '<', '<', '>', '>',
'>', '>', '>', '>', '>', '<', '<', '>', '>',
'>', '>', '>', '>', '>', '>', ' ', '>', '>',
'<', '<', '<', '<', '<', '<', '<', '=', ' ',
' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ',
'<', '<', '<', '<', '<', '<', '<', ' ', '='
};
| 栈顶\当前 | + | - | * | / | ^ | ! | ( | ) | \0 |
|---|---|---|---|---|---|---|---|---|---|
| + | > | > | < | < | < | < | < | > | > |
| - | > | > | < | < | < | < | < | > | > |
| * | > | > | > | > | < | < | < | > | > |
| / | > | > | > | > | < | < | < | > | > |
| ^ | > | > | > | > | > | < | < | > | > |
| ! | > | > | > | > | > | > | > | > | |
| ( | < | < | < | < | < | < | < | = | |
| ) | |||||||||
| \0 | < | < | < | < | < | < | < | = |
switch (orderBetween(optr.top(), *S))
{
// 查要看其与栈顶运算符之间优先级的高低
case '<': // 栈顶运算符优先级更低 比如栈顶加号 又来了个乘号
optr.push(*S); S++; break; // 计算推迟 当前运算符进栈 目光转向表达式的下一个字符
case '=': // 优先级相等 只有可能是栈顶为'(' 当前为')' 或者栈顶为'/0' 当前为'/0'
// 1 栈顶'(' 当前')'
// 这样一对括号彼此相逢 只可能是括号内的运算符都算完了
// 括号里只可能有数字 不会有运算符
// 它们直接消失就好了 栈顶'('也弹出 当前')'忽略 注意力转向表达式的下一个字符
// 2 栈顶'\0' 当前'\0'
// 最开始时 我们往栈底推入了一个'\0' 遇到了当前作为整个表达式结束标志的'\0'
// 将栈顶'\0'弹出 即栈清空 并将注意力跳过当前的\0字符
optr.pop(); S++; break;
case '>': // 栈顶运算符优先级更高 可以计算了 结果入栈 比如栈顶乘号 又来了个加号
char op = optr.pop(); // 弹出目前的栈顶操作符
if ('!' == op) // 阶乘 一元操作符
opnd.push(calcu(op, opnd.pop())); // 弹出操作数栈的栈顶 用这个操作符计算 计算结果推回到操作数栈
else
{
float pOpnd2 = opnd.pop (), pOpnd1 = opnd.pop(); // pOpnd2是后进先出
opnd.push(calcu(pOpnd1, op, pOpnd2)); // 这两个操作数用操作符计算
// 如果栈顶是3 第二靠近栈顶的是2 那么pOpnd2就是3 pOpnd1就是2 op是'\' 那就是计算2\3
// 不直接使用opnd.push(calcu(opnd.pop(),op,opnd.pop()))
// 因为这两个pop的求值顺序是未定义行为 具体怎样完全取决于编译器
}
break;
}
看一个例子
( 1 + 2 ^ 3 ! - 4 ) * ( 5 ! - ( 6 - ( 7 - ( 8 9 - 0 ! ) ) ) ) $
pri['$']['(']='<' (进操作符栈optr 数字1进操作数栈opnd
pri['(']['+']='<' +进栈 2进栈
pri['+']['^']='<' ^进栈 3进栈
pri['^']['!']='<' !进栈
而pri['!']['-']='>' -无法进栈
所以是时候计算栈顶操作符!了 弹出栈顶操作符!
现在
optr $ ( + ^ !
opnd 1 2 3
随着optr将栈顶!弹出 opnd的栈顶3也被弹出 !是一元操作符 则发生计算 3!=6 计算结果6重新放回栈中
optr $ ( + ^
opnd 1 2 6
此时我们注意力还在刚才仍未进栈的操作符-上
现在optr的栈顶是^ 而pri['^']['-']='>' 所以应该先算^ 这是一个二元操作符 pOpnd2 = 6 pOpnd1 = 2 弹出操作数 pOpnd1 op pOpnd2也就是2^6 计算结果64重新放回栈中
optr $ ( +
opnd 1 64
此时我们的注意力仍然在尚未进栈的操作符-上
现在optr的栈顶是+ pri['+']['-']='>' 应该先算+ 这是二元操作符 pOpnd2=64 pOpnd1=1 那么 pOpnd1 op pOpnd2就是1+64 计算结果65重新放回到栈中
optr $ (
opnd 65
此时我们的注意力还是在尚未进栈的操作符-上
现在optr的栈顶是( pri['(']['-']='<' pri['-'][]
[未完待续]